برز اسم شمس الدين السمرقندي كواحدٍ من ألمع علماء المسلمين في العصور الوسطى، وترك بصماته الخالدة في مجالاتٍ شتّى، لاسيما في مجال الهندسة. فما هي مساهماته في هذا العلم؟ وكيف أثرت أعماله على تطوّره؟
Table of Contents
السمرقندي بين النشأة والتعليم:
ولد شمس الدين السمرقندي في مدينة سمرقند في آسيا الوسطى عام 1221 م، ونشأ في بيئةٍ علميةٍ غنيةٍ شجّعت على التعلّم والبحث. تعلّم السمرقندي على يد كبار علماء عصره، وتلقّى علومًا متنوعةً شملت الرياضيات والفلك والمنطق والفلسفة. برز نبوغه منذ صغره، فأتقن العلوم الشرعية والرياضيات، وبرع في علم الهندسة.
مساهماته في الهندسة:
يُعدّ السمرقندي من رواد علم الهندسة في العالم الإسلامي، فقد ألّف العديد من الكتب والمخطوطات القيّمة التي أثرت على تطوّر هذا العلم. من أهمّ مساهماته:
- كتاب “أشكال التأسيس”: شرح فيه 35 شكلاً من أشكال كتاب “العناصر” لإقليدس، وبيّن تطبيقاتها الهندسية المختلفة.
- كتاب “موجز في علم الفلك”: قدّم فيه شرحًا مبسطًا لمبادئ علم الفلك وحسابات الأجرام السماوية.
- فهرس النجوم: قام بوضع فهرسٍ شاملٍ للنجوم في عامي 1276 و 1277 م، ساهم بشكلٍ كبيرٍ في تطوير علم الفلك.
- رسالة في أدب الباحث: ناقش فيها آداب البحث العلمي وطرق التحقيق الفكري.
السمرقندي مُؤسّس “علم الكلام الهندسي”:
تميّزت أعمال السمرقندي بِاعتمادها على الأشكال الهندسية لشرح الظواهر الكونية، ممّا جعله يُعدّ مؤسّسًا لما يُمكن تسميته بِـ “علم الكلام الهندسي”. فقد سعى السمرقندي إلى ربط علم الكلام بالرياضيات والهندسة، واستخدامها في تفسير العقائد الدينية.
تأثيره على العلماء:
أثرت أعماله على علماء المسلمين بشكلٍ كبيرٍ، ونُقّلت وترجمت إلى اللغات الأوروبية، ممّا ساهم في نقل المعرفة العلمية إلى الغرب. كما استفاد من أعماله العديد من العلماء الغربيين، مثل نيكولاس كوبرنيكوس وجاليليو جاليلي.
كتب السمرقندي كتاب «رسالة في أدب البحث» وناقش فيها نظريّة التحقق العلمي في التفكير باستخدام الجدلية، استخدم الإغريق القدماء طرق الاستقصاء والبحث هذه بشكلٍ كبير. كتب السمرقندي أيضاً كتاب «موجز في علم الفلك» وأصدر في عام 1276-1277 فهرساً للنجوم.
واحدة من أبرز صفات العمل الخاصّ بالسمرقندي هو أنّها قائمة على فكرة عرض الكون بالاعتماد على الأشكال الهندسيّة، ومن هذا المنطلق يمكن اعتباره مؤسّس الحركة التي من الممكن أن نطلق عليها اسم «علم الكلام الهندسي» في العالم الإسلاميّ.
اشتُهر السمرقندي في مجال علم الرياضيّات لنشره كتاباً من 20 صفحة فقط ناقش فيه 35 فرضيّة من فرضيات إقليدس. على الرّغم من صغر حجم العمل إلأ أن السمرقندي قد اطّلع على العديد من أعمال العلماء المسلمين في الرياضيّات قبل الشروع في كتابته. فعلى سبيل المثال أشار إلى كتابات كلّ من ابن الهيثم، وعمر الخيّام، والجوهري، ونصير الدين الطوسي، وأثير الدين الأبحري كمراجع لكتابه. قرأ العديد من علماء الرياضيّات في وقت لاحقٍ كتاب السمرقندي ذي العشرين صفحة، وأشاروا إليه كمرجعٍ في كتاباتهم، كما فعل العالم قاضي زادة في أحد كتبه.
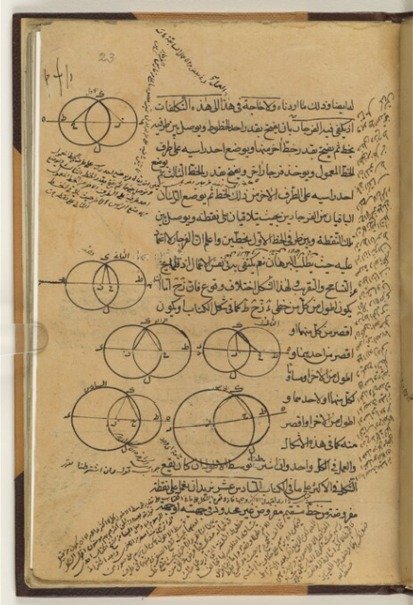
أساليب الاثبات الرياضي التي استخدمها السمرقندي
بحسب الباحث، فقد استخدم السمرقندي طرقا مختلفة ومبتكرة أحيانا، لإثبات هذه النظريات الهندسية. من بينها طريقة الاثبات بالتناقض التي استخدمها مرارا وتكرارا في العديد من البراهين، ذاكرا على سبيل المثال أنه “إذا تساوت زاويتان في المثلث، كانت الأضلاع المتجاورة متساوية“. وعلى الرغم من أن السمرقندي استخدم أساليب رياضية علمية لإثبات فرضيته حول نظريات هندسية مختلفة، فأنه اعتمد في بعض الحالات على المنطق المشترك دون دليل علمي واضح، فعلى سبيل المثال، خلص في نهاية معالجة أحد النظريات أنه: “إذا كان كل ضلع في مثلث يساوي كل ضلع في مثلث آخر فإن الزوايا المقابلة لها ستكون متساوية وسيكون المثلثان متساويين“.
كما تمكن السمرقندي من اثبات العديد من الخصائص الهندسية باستخدام برهان مبتكر لم يسبق له مثيل من قبل علماء الرياضيات الآخرين. فعلى سبيل المثال، وعند محاولته إثبات تساوي مساحات متوازيي أضلاع دون استخدام صيغة حساب المساحات الهندسية، ذكر أن “كل سطحين متوازيي أضلاع يشتركان في قاعدة واحدة في ضلع واحد بين خطين متوازيين هما متساويان“.
رغم أن هذا الكتاب شكل مرجعا لدراسة الهندسة لعدة قرون في المدارس العربية وساهم في نشر هذا العلم في التراث العلمي العربي المكتوب، فأنه لم يدرس بشكل دقيق، كما يقول الباحث في دراسته المنشورة حديثا، ولم يتم تقديمه بشكل يتناسب مع أهميته في الأدبيات العلمية العربية الحديثة.
وعموما، كان السمرقندي أحد العلماء الذين أثرت أعمالهم بشكل كبير في تراث العلوم العربية وتستحق مؤلفاته دراسة عميقة من قبل مؤرخي العلوم والعلماء العرب بدلا من تركها للأجانب، الذين يواجهون أحيانا صعوبات في فهم اللغة المستخدمة في هذا العصر، من أجل إدراك الدور الذي لعبه هذا العالم في مجاله.
خاتمة:
لا شكّ أنّ شمس الدين السمرقندي كان من كبار علماء عصره، وترك إرثًا علميًا غنيًا ساهم في تطوّر العلوم المختلفة، لاسيما علم الهندسة.